Medidas de Tendencia Central
Supóngase que Pedro obtiene 32
puntos en una
prueba de lectura. La calificación por sí misma tiene muy poco significado a menos que usted conozca cuál es el total de puntos que obtiene una presona
promedio al participar en esa prueba, cuál es la calificación menor
y
mayor que se obtiene, y cuán variadas son esas calificaciones. Es decir que para que una calificación tenga significado hay que
contar con elementos de referencia generalmente relacionados con ciertos
criterios estadísticos.
Las medidas de tendencia
central (media, mediana y
moda ) sirven como puntos de referencia para
interpretar las calificaciones que se obtienen en una prueba. Digamos por ejemplo que la calificación promedio en la prueba que hizo Pedro fue de 20 puntos. De ser así podemos decir que la calificación de Pedro se ubica notablemente sobre el promedio. Pero si la calificación promedio fue de 60 puntos, entonces la
conclusión sería muy diferente, dado que se ubicaría muy por debajo del promedio de la
clase.
En resumen, el propósito de las medidas de tendencia central es:
- Mostrar en qué lugar se ubica la persona promedio o típica del grupo.
- Sirve como un metodo para comparar o interpretar cualquier puntaje en relación con el puntaje central o típico.
- Sirve como un método para comparar el puntaje obtenido por una misma persona en dos diferentes ocasiones.
- Sirve como un método para comparar los resultados medios obtenidos por dos o más grupos.
La media aritmética de una variable se define como la suma ponderada de los valores de la variable por sus frecuencias relativas y lo denotaremos por
y se calcula mediante la expresión:
xi representa el valor de la variable o en su caso la marca de clase.
Propiedades:
- Si multiplicamos o dividimos todas las observaciones por un mismo número, la media queda multiplicada o dividida por dicho numero.
- Si le sumamos a todas las observaciones un mismo número, la media aumentará en dicha cantidad.
- Además de la media aritmética existen otros conceptos de media, como son la media geométrica y la media armónica.
La mediana es el punto central de una
serie de datos, para datos agrupados la mediana viene dada por:
Ejemplo:
Hallar la mediana en los siguientes datos: 25,30,28,26,32
Solución:
Se ordenan en forma creciente o decreciente y se toma el
valor central. 25,26,28,30,32
mediana = 28
Ejemplo:
Hallar la mediana en los siguientes datos 7, 10,15,13,10,12
Solución:
Al ordenar se tiene: 7, 10,10,12,13,15 pero como el número de datos es par se toma la media aritmética de los dos internos.
La
moda es el valor de la variable que tenga mayor frecuencia absoluta, la que más se repite, es la única medida de centralizacion que tiene sentido estudiar en una variable cualitativa, pues no precisa la realización de ningún calculo.
Por su propia definición, la moda no es única, pues puede
haber dos o más
valores de la variable que tengan la misma frecuencia siendo esta máxima. En cuyo caso tendremos una
distribución bimodal o polimodal según el caso.
Para distribuciones de frecuencia la moda viene dada por:
Ejemplo:
Hallar la moda en los siguientes datos.
16,18,15,20,16
Solución:
Moda = 16
De estas tres medidas de tendencia central, la media es reconocida como la mejor y más útil. Sin embargo, cuando en una distribución se presentan casos cuyos
puntajes son muy bajos o muy altos respecto al resto del grupo, es recomendable utilizar la mediana o la moda.
Representaciones Gráficas
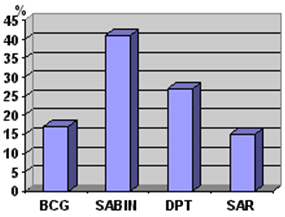
Se utilizan rectángulos separados, que tienen como base a cada uno de los datos y como altura la frecuencia de ese dato.
Ejemplo: En la siguiente tabla se muestra el total de vacunas aplicadas durante el
verano de l991 en un estado de la República Mexicana.
El diagrama de barras o gráfica de barras suele elaborarse con algunas
variantes; por ejemplo, se pueden utilizar líneas en vez de rectángulos ó barras (o líneas) horizontales en vez de verticales.
Si se tienen datos cuantitativos se grafica en el eje de las x los valores
centrales ( marcas de clase), cuyas alturas son proporcionales a sus frecuencias. Así en la distribución de frecuencias de las alturas de 35 alumnos se tiene:
El histograma es un gráfico para la distribución de una variable cuantitativa continua que representa frecuencias mediante el volumen de las áreas. Un histograma consiste en un conjunto de rectángulos con:
a.
bases en el eje horizontal,
centros en las
marcas de clase y longitudes
iguales a los tamaños de los intervalos de clase
b. áreas proporcionales a las frecuencias de clase.
En el caso de un histograma para intervalos desiguales sólo se señalizan los valores sobre el eje horizontal, el eje vertical no tiene sentido porque las frecuencias corresponden al área de cada rectángulo.
Si en la distribución se toman
clases de la misma longitud, las frecuencias son proporcionales a las alturas de los rectángulos del histograma ya que el área se obtiene multiplicando la base por la altura por lo que queda similar a un diagrama de barras,
solo que
ahora las barras van una junto a otra por tratarse de una variable continua
El polígono de frecuencias es una
representación gráfica de la distribución de frecuencias que resulta esencialmente equivalente al histograma y se obtiene uniendo mediante segmentos los centros de las bases superiores de los rectángulos del histograma (es decir, los puntos de las marcas de clase).
Para cerrar la figura, se une la
línea quebrada con lo que sería la
marca de clase (sobre la superficie del eje horizontal) anterior a la
primera y posterior a la última registrada
Polígono de Frecuencias Acumuladas u Ojiva
La misma idea de unir los centros de las bases superiores de los rectángulos de la distribución del histograma de frecuencias
acumuladas, da lugar al polígono de frecuencias acumuladas u ojiva.
